Парадокс невозможности демократии

Ниже - глава из книги Эдварда Шейнермана «Путеводитель для влюбленных в математику» — о том, как работают правило большинства и правило диктатора, а также почему так сложно учесть интересы всех.

Выбор в случае двух кандидатов

Знакомая всем демократическая процедура — выборы, на которых два кандидата претендуют на одну и ту же должность. Избиратели отдают голоса за первого или второго кандидата, и побеждает тот, кто наберет больше голосов.

Ключевая фраза: побеждает тот, кто наберет больше голосов — краеугольный камень демократического общества. Но насколько справедлив этот принцип?

Более сложная система выборов подразумевает, что избиратели отмечают, насколько сильно они предпочитают одного кандидата другому.

Вообразим, что два кандидата, претендующих на одну и ту же должность, зовутся A и B. Избиратели отдают голос за того или другого*.

Если отдано n голосов, данные голосования выглядят следующим образом:

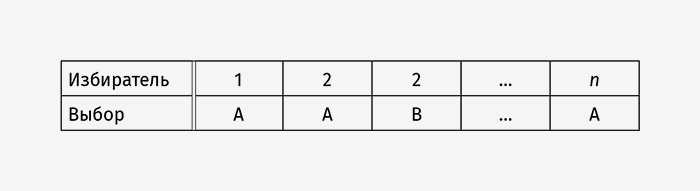
Мы будем использовать термин «профиль предпочтений» для совокупности индивидуальных голосов.

Как используется такой профиль предпочтений* для принятия решения? Обычно просто подсчитывают, сколько голосов было отдано за каждого кандидата. Победителем оказывается тот, кто набрал больше голосов. Мы назовем такой подход правилом большинства — это метод демократических сообществ. Но это не единственный метод учета профиля предпочтений для принятия решения. Посмотрим на альтернативы.

Правило диктатора подразумевает, что решение принимается на основе голоса одного-единственного человека, скажем избирателя No 1. Если No 1 выбирает A, побеждает A; если No 1 выбирает B, побеждает B. Другие мнения не учитываются.

Мы будем называть правило большинства и правило диктатора методами принятия решений. На входе — голоса избирателей, на выходе — решение о победе того или другого кандидата. В мире используют оба метода, но правило диктатора считается нечестным. Почему?

Важно не смешивать метод принятия решения (например, правило большинства) со свойствами, которыми он обладает (например, нейтральность учета голосов). Разные методы могут обладать каким-то одним свойством, но отличаться другими. Мы высвечиваем разницу, используя полужирное начертание для обозначения метода и курсив для обозначения свойства.

Для вящей справедливости метод принятия решения должен обладать определенными свойствами. Обидная особенность правила диктатора заключается в том, что голоса не учитываются равным образом. Более формально: справедливый метод принятия решения должен следовать нейтральности учета голосов* — не важно, кто голосует, важно, сколько голосов отдано за того или другого кандидата. Правило большинства отвечает требованию нейтральности учета голосов, а правило диктатора — нет.

Если мы руководствуется только теми методами, которые обладают свойством нейтральности учета голосов, мы просто суммируем голоса, отданные за того или другого кандидата. Итоговая статистика может выглядеть следующим образом:

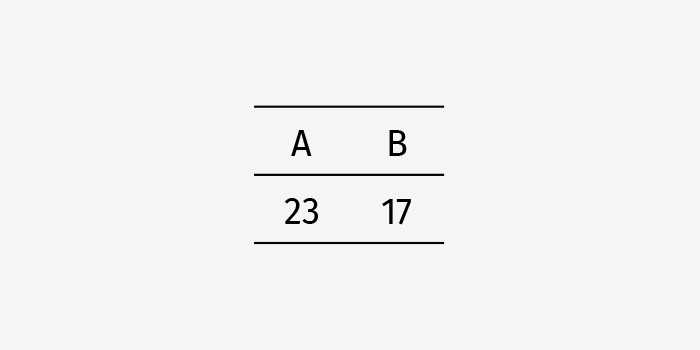
Есть и другой метод. Назовем его правилом алфавита. Побеждает тот кандидат, чье имя идет первым по алфавиту. Тогда в любом случае побеждает кандидат A. Очевидно, и этот метод несправедлив, но почему?

Отмечу, что правило диктатора удовлетворяет требованию нейтральности учета кандидатов.

Он обладает свойством нейтральности учета голосов: все избиратели равны в том плане, что не учитывается ничье мнение! Проблема состоит в том, что кандидаты поставлены в неравное положение. Мы будем говорить, что метод обладает свойством нейтральности учета кандидатов*, если к кандидатам относятся одинаково; если кандидат сменит имя, это не повлияет на итог выборов.

Чувство справедливости требует нейтральности учета голосов и нейтральности учета кандидатов. Достаточно ли этого?

Есть еще один метод, который мы будем называть правилом нечетности: победу одерживает тот кандидат, который набрал нечетное число голосов. Если A предпочли 20 избирателей, а B — 13 избирателей, побеждает B. Этот метод отвечает требованиям нейтральности учета голосов и нейтральности учета кандидатов.

Или рассмотрим правило меньшинства: побеждает тот, кто набрал меньше всего голосов. Если A предпочли 12 избирателей, а B — 30 избирателей, побеждает A. Этот метод также отвечает требованиям нейтральности учета голосов и нейтральности учета кандидатов.

Два требования, нейтральность учета голосов и нейтральность учета кандидатов, исключают некоторые нечестные методы (такие как правило диктатора и правило алфавита), но кое-какие несуразные методы отвечают тому и другому требованию. Введем новое свойство, позволяющее отсеять разумные методы (такие как правило большинства) от несуразных.

Вот в чем заключается проблема с правилом нечетности. Вообразим, что профиль предпочтений следующий:

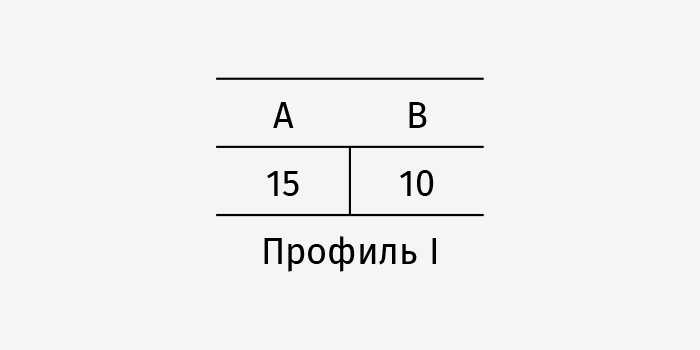
Если руководствоваться правилом нечетности, побеждает A. Теперь предположим, что один избиратель передумал, забрал свой голос за B (проигравшего) и отдал A (победителю). Передумал всего лишь один избиратель; другие остаются при своем мнении. Итог таков: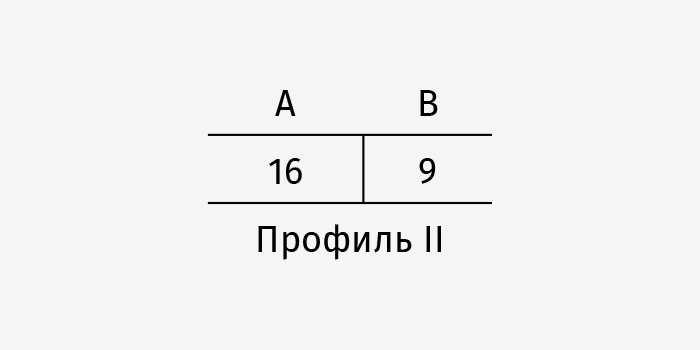

Правило нечетности приводит B к победе.

Вот формальное определение монотонности. Мы называем метод принятия решений монотонным, если перемена решения одного избирателя в пользу победителя не меняет итога выборов.

Нечестно! Если один избиратель меняет свое мнение и предпочитает победителя проигравшему, это не должно влиять на результат. Правило нечетности нарушает требование монотонности*. Есть еще одна проблема с правилом нечетности. Что произойдет, если избирателей четное количество? Рассмотрим две ситуации:

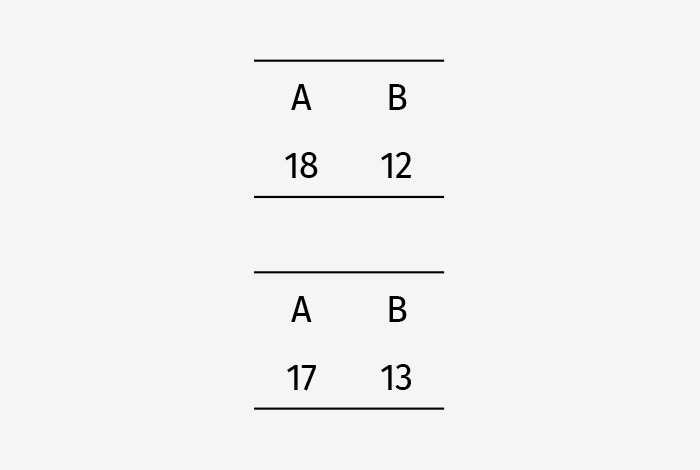
В первом случае победителей нет, во втором случае побеждают оба кандидата. В том или ином случае мы заходим в тупик.
Желательно избегать тупиковых итогов на выборах, чтобы коллективное мнение избирателей приводило к определенному решению. Некоторые методы (такие как правило диктатора) никогда не создают таких проблем. Но некоторые методы, отвечающие требованиям нейтральности учета голосов и нейтральности учета кандидатов, тоже могут завести в тупик: например, если голоса избирателей распределились поровну.

Даже если мы накладываем условия нейтральности учета голосов и нейтральности учета кандидатов, половина голосов может уйти первому кандидату, а другая половина — второму, так что нельзя будет принять внятное решение. Такое вероятно даже в случае правила большинства.

Правило диктатора, конечно, однозначное: оно никогда не заводит в тупик.

Однако оно не позволяет выбрать победителя в одной-единственной ситуации. Мы будем говорить, что этот метод в целом однозначный, так как позволяет принять решение во всех случаях, кроме одного: когда голоса распределились поровну*.

Правило меньшинства тоже в целом однозначное (но не монотонное). Мы определили четыре свойства справедливых выборов: нейтральность учета голосов, нейтральность учета кандидатов, монотонность и однозначность. К счастью, правило большинства обладает всеми этими свойствами. Занесем результаты в таблицу:

Кеннет Мэй (1915–1977) — американский математик, экономист и историк математики. Защитил диссертацию по математической теории трудоустройства. Придерживался коммунистических взглядов. В терминологии Мэя четыре свойства — нейтральность, анонимность, положительный отклик и однозначность.

Но ведь должны быть альтернативы! Есть ли другие методы принятия решений, отвечающие всем четырем требованиям? Ответ отрицательный. В 1952 году Кеннет Мэй доказал, что правило большинства — единственный метод, обладающий всеми четырьмя свойствами*.

Выбор в случае более чем двух кандидатов

Наше интуитивное предчувствие, что правило большинства справедливее всего, подтвердилось со всей математической строгостью. Теорема Мэя говорит о том, что для выборов в случае двух кандидатов есть всего лишь один разумный метод.

Ситуация существенно меняется, если число кандидатов возрастает. Но мы все еще вправе надеяться, что методы вроде правила большинства остаются эффективны.

Начнем с описания того, как именно избиратели отдают голоса. Если кандидатуры выдвинули три (или больше) человека, каждый избиратель должен ранжировать их в своем бюллетене. Статистика может выглядеть так:

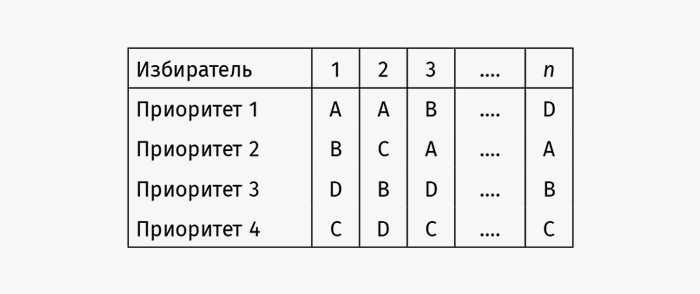
Я максимально упрощаю ситуацию. Можно себе представить, что избиратель симпатизирует A, равнодушен к B и C и полностью отвергает кандидатуру D. Так или иначе, мы рассчитываем, что избиратель все-таки ранжирует их. Математики рассматривают более сложные ситуации, но мы с вами ограничимся самой простой моделью.

Как и раньше, мы ищем методы принятия решений, учитывающие распределение голосов на входе, а на выходе выносящие решение о победителе. Например, правило диктатора подразумевает, что победа достанется тому, кто возглавляет список предпочтений одного-единственного избирателя No 1. В нашем случае это кандидат A. Прочие голоса игнорируются. Правило диктатора не отвечает требованию нейтральности учета голосов (хотя требование нейтральности учета кандидатов здесь выполняется). Вероятно, разумнее руководствоваться методами, нейтрально учитывающими голоса, и посчитать, каков приоритет того или иного кандидата для каждого избирателя. Например, в случае трех кандидатов* итоговая статистика выглядит так:

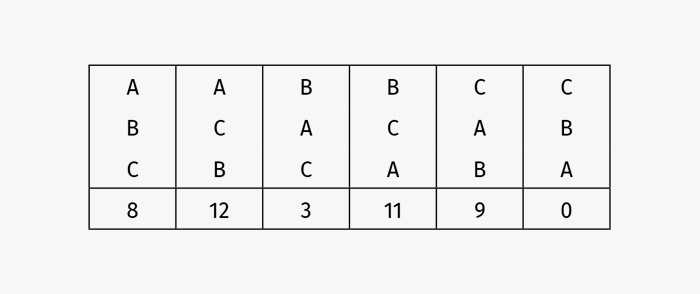
Согласно этой статистике, 20 человек поставили на первое место A, 14 предпочли B, 9 предпочли C. Как нам выбрать победителя?
Правило большинства хорошо подходит, когда кандидатов двое. В случае трех кандидатов перевес возникает тогда, когда больше половины избирателей поставили на первое место одного кандидата. Это происходит не всегда, потому руководствоваться правилом большинства становится проблематично. Кроме того, правило большинства не учитывает распределение приоритетов второй и третьей степени. Посмотрим, насколько это важно. Проанализируем следующий профиль предпочтений:

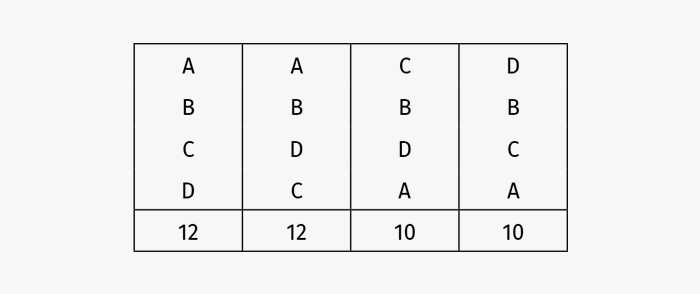
Отмечу, что больше половины избирателей поставили на первое место A. Следует ли из этого, что отдать победу A — лучший выбор? А что значит «лучший»? Математика ответить не в силах. Для нас справедливо то, что соответствует нашей системе ценностей. Проиллюстрируем это обстоятельство. Вообразим, что «кандидаты» у нас — рестораны, а «избиратели» — офисные клерки, ищущие место для проведения корпоратива. Вот информация о ресторанах: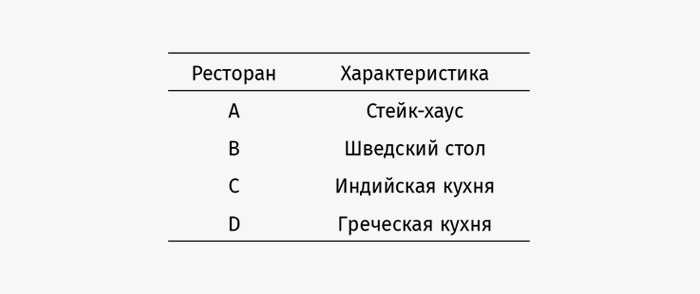

Ситуация вполне реальная. Большинство клерков (24 человека) предпочитает поужинать в стейк-хаусе, но значительное число (20 человек) не любит стейки. Индийская и греческая кухня остались в меньшинстве, но собрали равное число голосов. Однако абсолютно все отметили ресторан со шведским столом в качестве второго приоритета. Это выглядит хорошим компромиссом, и мудрый босс выбирает заведение со шведским столом для корпоратива.

Можно ли построить аналогичный метод принятия решения на выборах?

Существует множество методов для проведения выборов, когда кандидатов более двух. Правило большинства идеально подходит в случае выборов среди двух кандидатов, но в других ситуациях кандидат может не получить больше 50% голосов и, как показывает наш пример с ресторанами, тогда становится неясно, как принять «верное» решение. Давайте обсудим несколько методов принятия решений и выясним, какой из них лучше. Будем использовать следующий профиль предпочтений:

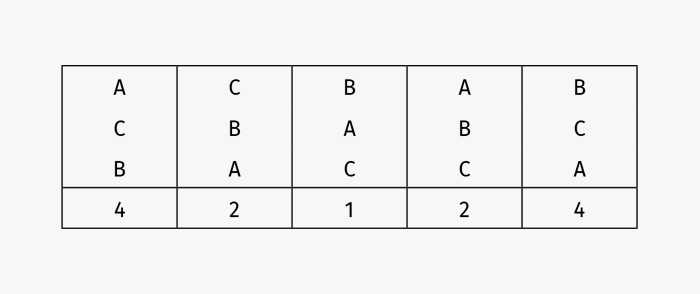
Профиль предпочтений в случае трех кандидатов

Правило большинства. Это наиболее распространенный метод. Мы выясняем, за какого кандидата отдано наибольшее число голосов, причем не обязательно больше половины. В вышеуказанном профиле предпочтений кандидата А выбрало наибольшее число избирателей (шесть), затем идет В (пять), на последнем месте С (два). По правилу большинства побеждает А.

Правило первых двух приоритетов. Проблема правила большинства состоит в том, что оно не учитывает рейтинг предпочтений. Правило первых двух приоритетов основано на подсчете того, как много избирателей поставили кандидата на первое или второе место. Для вышеуказанного профиля предпочтений:

• ― A получил 6 + 1 = 7 голосов (шесть раз на первом месте и один раз на втором);
• ― В получил 5 + 4 = 9 голосов (пять раз на первом месте, четыре раза на втором);
• ― С получил 2 + 8 = 10 голосов (дважды на первом месте и восемь раз на втором).

Таким образом, по правилу первых двух приоритетов побеждает С.

Этот метод назван в честь Жана-Шарля де Борда, французского математика XVIII века. Подсчет по методу Борда в случае четырех кандидатов делается так: первый приоритет избирателя приносит кандидату 3 очка, второй — 2, третий — 1, четвертый — 0 очков. Количество очков в случае пяти кандидатов будет 4, 3, 2, 1 и 0 соответственно. Обратите внимание, что в случае двух кандидатов метод Борда ничем не отличается от правила большинства.

Метод Борда. Если мы руководствуемся правилом большинства, то не учитываем, кого каждый избиратель ставил на второе место. В правиле первых двух приоритетов второй приоритет имеет тот же вес, что и первый. Метод Борда — компромисс между ними*.

Он заключается в том, что первый приоритет избирателя приносит кандидату 2 очка, второй приоритет — 1 очко, третий приоритет — ни одного очка. Дальше мы складываем очки. Побеждает тот кандидат, у кого их окажется больше. Давайте проанализируем, как работает метод Борда в случае рассмотренного выше профиля предпочтений:

• ― кандидат A имеет первый приоритет у шести избирателей и второй — у одного, таким образом, он набирает 6 × 2 + 1 × 1 = 13 очков;
• ― кандидат B имеет первый приоритет у пяти избирателей и второй — у четырех, таким образом, он набирает 5 × 2 + 4 × 1 = 14 очков;
• ― кандидат C имеет первый приоритет у двух избирателей и второй — у восьми, таким образом, он набирает 2 × 2 + 8 × 1 = 12 очков.

В соответствии с методом Борда победителем станет кандидат B. Нарисуем сводную таблицу победителей для одного и того же профиля предпочтений при использовании трех разных методов:

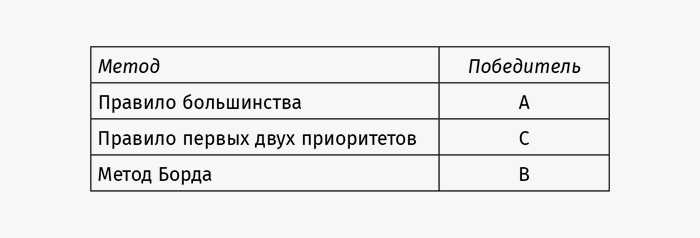
Результат обескураживает. Сложно обвинить какой-либо из трех методов в нелепости (в отличие от правила нечетности или правила меньшинства). Все три подхода удовлетворяют критериям честности: им свойственны нейтральность учета избирателей, нейтральность учета кандидатов и монотонность, потому нельзя отбраковать хотя бы один из них на этом основании. Может быть, мы найдем еще какой-нибудь критерий честности, чтобы выбрать «наилучший» метод?

Независимость от посторонних альтернатив

Последний критерий справедливости, который я рассмотрю в этой главе, называется независимость от посторонних альтернатив. Он носит более изощренный характер, чем другие критерии, поэтому я начну с простого примера. Вообразите, что ваша подруга выбирает десерт после ужина в ресторане. В меню указаны три варианта: торт, пирог и мороженое. Девушка заказывает мороженое. Официант, приняв ее заказ, говорит вам: «О, похоже, у нас закончились пироги». Тут девушка отвечает: «В таком случае я закажу торт!»

Что за чушь? Если она предпочитает мороженое (а не торт и не пирог), нет никакой разницы, остались ли в ресторане пироги. Но перемена выбора вашей подружки связана именно с фактом отсутствия пирогов, это не совпадение. Есть искушение заподозрить, все ли у нее в порядке с головой!

Мы ожидаем, что методы принятия решений будут разумными. Допустим, некий метод провозглашает кандидата X победителем на основании определенного профиля предпочтений. Допустим также, что другой кандидат, Y, снимает свою кандидатуру (и ни один избиратель не меняет своего мнения). В таком случае X должен остаться победителем. Если метод удовлетворяет такому условию, это и есть независимость от посторонних альтернатив.

Подумаем в том же ключе о правиле большинства. Для рассмотренного выше профиля предпочтений этот метод провозглашает победителем A. Теперь представим, что C снимает кандидатуру. Профиль предпочтений меняется следующим образом:

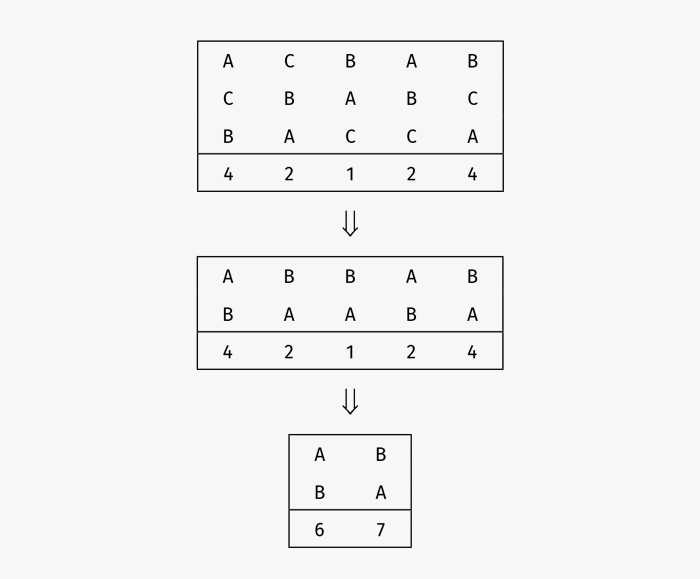
На сей раз победителем становится кандидат B! Таким образом, правило большинства не удовлетворяет критерию независимости от посторонних альтернатив. Может быть, правило первых двух приоритетов лучше? На основе того же профиля предпочтений победителем становится C. Что произойдет, если A сойдет с дистанции? Останется всего два кандидата! Тут мы заходим в тупик. Вот вам головоломка: попробуйте составить такой профиль предпочтений при голосовании за четырех кандидатов (A, B, C, D), чтобы правило первых двух приоритетов провозглашало победителем A, но если бы из гонки выбыл D, победителем стал бы B. Ответ я дам в конце главы.
Наконец, протестируем метод Борда. Он провозглашает победителем B, но если C выбывает, победителем становится A. Ни один из трех методов не удовлетворяет критерию независимости от посторонних альтернатив.

Спокойствие, только спокойствие! Есть множество других методов. Разумеется, какие-нибудь из них удовлетворяют критерию независимости от посторонних альтернатив. Например, правило диктатора (если кандидат A имеет первый приоритет у избирателя No 1, он останется победителем, кто бы из других кандидатов ни выбыл из игры). Разумеется, правило диктатора — не лучший метод, потому что не удовлетворяет одному из основных критериев — нейтральности учета избирателей.

 Кеннет Джозеф Эрроу (1921–2017) — американский экономист, лауреат Нобелевской премии по экономике за 1972 год «за новаторский вклад в общую теорию равновесия и теорию благосостояния».

Возникает вопрос: какой из справедливых методов голосования удовлетворяет критерию независимости от посторонних альтернатив? Ответ был найден Кеннетом Эрроу* в 1950 году: увы, но такого метода нет.

Теорема невозможности Эрроу носит несколько технический характер, но ее смысл заключается в том, что при наличии более чем двух кандидатов ни один метод не удовлетворяет базовому критерию независимости от посторонних альтернатив*.

Точнее, ни один метод не удовлетворяет одновременно четырем критериям: нейтральности учета избирателей, нейтральности учета кандидатов, монотонности и независимости от посторонних альтернатив. 

Как нам теперь быть? Если все методы «несправедливы», каким из них нам руководствоваться? Или просто нужно отбросить критерий независимости от посторонних альтернатив? Нанесет ли это большой вред?

Проблема методов, не удовлетворяющих последнему критерию, заключается в том, что они поощряют избирателей голосовать иначе, чем они планировали изначально, если какой-нибудь кандидат портит шансы вероятного победителя. Например, вам по душе кандидаты A и B, но вы питаете отвращение к кандидату C. Вы склоняетесь к тому, чтобы голосовать за A, но внезапно узнаете из выпуска новостей, что шансы A на победу невелики. За кого вы будете голосовать? При подсчете голосов по правилу большинства (и при использовании некоторых других методов) неразумно голосовать за A, хотя изначально вы планировали поступить именно так. Если вы проголосуете за A, то отнимете один голос у B.

Если A не выбывает из игры, а избиратели, чьи изначальные приоритеты совпадают с вашими, не меняют своего решения и все-таки голосуют за A, это отнимает голоса у B и обеспечивает победу C. Но если A по тем или иным причинам выбывает из игры, вы голосуете за B, и его шансы на победу возрастают.

Если метод принятия решений удовлетворяет критерию независимости от посторонних альтернатив, такой дилеммы не возникает. Вы можете голосовать, как и планировали, потому что выбор в пользу A не обесценит вашего голосования.

Парадокс Эрроу

Эрроу математически доказывает, что реальная демократия не может быть полной.

В 1972 году Нобелевскую премию по экономике присудили американскому математику Кеннету Эрроу за исследование «Социальный выбор и индивидуальные ценности». Под таким скромным названием в наш мир вошло сенсационное открытие, положившее конец мечтам об идеальной демократии. Выделив пять непременных условий демократическиx выборов как механизма выявления воли большинства избирателей, Эрроу доказал: в принципе невозможна избирательная система, в которой не нарушалось бы, по крайней мере, одно из этих условий! Это открытие произвело впечатление разорвавшейся бомбы.

«Оказывается, лучшие умы человечества занимаются поисками химеры, зиждущейся на внутреннем логическом противоречии исходных принципов, - писал один из тогдашних обозревателей. - Теперь учёные во всем мире пытаются спасти то, что может быть спасено от разрушительного открытия Эрроу, занявшего в математической политологии такое же место, какое занимает в математической логике открытая Куртом Гёделем в 1931 году теорема о невозможности построения непротиворечивой математической теории, содержащей аксиомы арифметики...».

Справедливости ради заметим: американец сделал своё открытие не на пустом месте. С дефектами демократической системы выявления воли большинства путём подсчёта голосов столкнулся в XVIII веке маркиз Кондорсе (1743-1794 гг.), философ, математик и политический деятель, казнённый во время Французской революции. Позднее так называемый парадокс Кондорсе переоткрыл на материалах выборов в Оксфордском университете Льюис Кэрролл.

В 1940-х годах подобным же наблюдением озадачил политиков английский экономист Л. Блэк, исследовавший эффективность принятия решений во всякого рода комитетах. Открытие Эрроу прояснило вопрос, но не облегчило практические поиски разрешения тупиковых ситуаций. Теперь эксперты гадают, от какого из пяти условий можно отказаться, не развалив существующие системы голосования.

Тем временем другие специалисты обращаются к историческому опыту. Ведь народы мира, далекие от понимания математических тонкостей, давно нашли практические пути разрешения тупиковых ситуаций, порождаемых играми в демократию. На место запутавшихся в неувязках парламентариев народы всегда выдвигали диктаторов, которые своей единоличной властью исполняли требования жизни. Но вот вопрос: как приводить к власти такого диктатора?

Специалисты по принятию решений (оказывается, на 3ападе есть такие!) рекомендуют диктатора избирать демократическим путём. Но ведь это очередная логическая нелепица! Диктаторов голосованием не избирают. Они приходят сами, но при всенародном одобрении...

Когда выбираешь какое-то действие, ты выбираешь и последствия этого действия

Наткнувшись на «теорему невозможности» К.Дж. Эрроу, невозможно было удержаться от того, чтобы, как выразился один знакомый, не «поточить об неё рога». Суть её в том, что способ голосования может быть избавлен от произвольности, безвыходных положений или неравноправия, но не может избежать этих недостатков одновременно.

Самая правильная система выборов в самом демократичном обществе способна привести к ситуации равновесия предпочтений голосующих, которая неразрешима демократическими средствами, а диктаторские недопустимы по определению. Теорема описана и комментируется так, как будто она – краеугольный камень демократии. То есть, Эрроу математически доказывает, что реальная демократия не может быть полной.

Но действительно ли идеал демократии сводится к математической модели процедуры голосования, избавленной от произвольности, безвыходных положений и неравноправия? Или это просто красивая теория, не имеющая отношения к реальности? Действительно ли демократия исключает произвол или неравноправие? Увы, не исключает даже теоретически. Например:

• 1. Не все признаются гражданами.
• 2. Не все граждане имеют право голоса.
• 3. Не все граждане, имеющие право голоса, могут быть выдвинуты.
• 4. Значимость одних и тех же критериев у разных граждан всегда будет различаться, равно как и осведомлённость о соответствии кандидатов этим критериям. Отсюда следует неравная компетентность избирателей при равном «весе» их голосов.
• 5. Принципы демократии распространяются лишь на очень небольшую часть общественных отношений даже в самых образцово-показательных государствах, считающихся эталонами демократии, да и то лишь в ограниченное время в особых ситуациях. Во всём остальном предпочтение отдаётся диктатуре, явной или косвенной. Реальная демократия предусматривает не только равные права, но и неравные возможности в большей части областей жизни общества. Американцы, столь ревностно относящиеся к своим демократическим правам, равнодушны к разнице между выборами президента промышленной корпорации и президента «корпорации Америка».

Если разобраться по существу, аксиомы Эрроу есть сами по себе диктаторские правила голосования. Ограничения на число кандидатов и по их квалификации тоже вводятся вполне диктаторски. Как бы демократично не избирали парламент, но законы он будет вводить вполне диктаторски, не спрашивая мнения избирателей. По существу это означает необходимость переосмыслить понятие демократии.

Демократия – это выборы лучшего кандидата на роль руководителя какого-то проекта.

Тем самым подразумевается, что в обществе существует определённое неравенство в отношении способностей руководить этим проектом.

Возникает вопрос: могут ли те, кто разбирается хуже (прямо скажем, совсем не разбираются, судя по опыту с «кухарками»), выбрать того, кто разбирается лучше? А если не могут, то чего стоит их мнение и зачем вообще нужен выбор? Если граждане различаются по способности оценивать истинные критерии, то они должны различаться и по «весу» своего голоса. Эрроу не рассмотрел эту ситуацию: выбор должен производиться людьми, компетентными в работе, которую предстоит выполнять избранному, а избиратели таковыми не являются по определению.

Следовательно, они не в состоянии оценивать по истинным критериям пригодность кандидата. Отсюда следствие: право избирать должно быть уравновешено способностью оценивать. Не зря ведь в самых демократически продвинутых государствах часть категорий граждан не допускается к выборам по ряду причин. Например, дети: они слишком, видите ли, некомпетентны по сравнению со взрослыми (как будто немалая часть тех более компетентна).

Да и не существует естественная чёткая граница между имеющими право голосовать и не имеющими. Граница проводится вполне диктаторски, не спрашивая мнения избирателей.

Или вот, скажем, президентом США можно быть лишь два срока, а президентом Федеральной резервной системы США – пять. А ведь несколько слов последнего, оброненных в разговоре, имеют куда более серьёзные последствия.

Ради пущей демократии признано целесообразным существование института пожизненных судей с сугубо диктаторскими полномочиями. В том смысле, чтобы политическая конъюнктура не влияла на их профессионализм. Можно подумать, что те судьи живут на Луне. А разве другие государственные люди не должны проявлять свой профессионализм так же независимо?

Похожее по теме... Почему Германия поверила Гитлеру?Как получилось, что культурная нация смогла не только принять Гитлера, но даже не сопротивляться?

Вспомним реликтовую уже форму демократии – непосредственную, типа вече. Она предусматривала равноправие граждан при решении общих для них вопросов (теоретически, по крайней мере). Современная демократия (впрочем, ещё с античных времён) ограничила их равноправие всего одним вопросом: выбором тех, кто эти вопросы будет решать. И, соответственно, одним формальным вопросом: процедурой голосования.

Закономерен вопрос: а действительно ли т.н. выборная демократия есть власть народа? Вполне очевидно, что власть принадлежит тем, кому она принадлежит, а народ служит лишь в качестве одного из аргументов в споре претендентов на первые роли.

Но не будем особо заглубляться в политику, хотя обсуждаемая тема сама по себе – сплошная политика. Если рассмотрим проблему по существу, то увидим, что на самом деле теорема Эрроу представляет собой лишь расширенный и усложнённый вариант «буриданова осла» - задачи, которая в абстрактной форме не имеет решения, ибо она и сформулирована так, чтобы не иметь решения: если А=Б, то и Б=А.

Теорема Эрроу отличается лишь тем, что вместо одного осла имеем целое стадо равноправных ослов, а вместо двух стогов – несколько. По условиям игры ослы должны демократически проголосовать, к какому стогу сена идти (а идти должны все вместе). Конечно, вероятность тупика при выборе альтернатив у стада ослов меньше, нежели у одного осла. Но это несущественно, так как имеет значение лишь сама возможность возникновения неопределённости.

Собственно говоря, набор аксиом потребовался математику Эрроу лишь для того, чтобы принудить стадо ослов при оценке альтернатив вести себя как один осёл. То есть, Эрроу тщательно выписал правила, по которым равновесное (критическое) распределение равноправных голосов ослов будет не менее вероятно, чем любое иное. Поэтому вероятность возникновения равновесия между альтернативами сохраняется, как если бы размышлял лишь один осёл, оценивая варианты с разных точек зрения (при равенстве оценок по разным критериям).

Эрроу доказал, что выйти из равновесия можно только диктаторскими методами. Иначе говоря: если один осёл будет «несколько более равным», чем другие. Но шестая аксиома воспрещает одному из ослов диктаторски махнуть копытом на демократию и повести за собой стадо к ближайшему к нему стогу (все ослы ведь не могут поместиться в точке), выведя из демократического оцепенения остальных ослов. Или просто пойти туда, куда левая нога захочет.

На самом деле и диктатура сама по себе не есть решение проблемы выбора: что с того, что выбирать между равноценными альтернативами придётся не стаду ослов, а одному ослу, пусть и самому крутому? Один осёл – он сам себе диктатор. Проблема не в голосовании как таковом, а в выборе среди альтернатив, равноценных по какой-то группе критериев.

В реальности живой осёл (как и любое иное живое существо, кроме человека) ни на секунду не замешкается, так как природа встроила в него механизм нарушения равновесия между равными предпочтениями: осёл пойдёт налево. У человека тоже есть такой механизм, но его действие можно увидеть лишь изредка. Например, если человек, оказавшись без компаса в густом тумане, попытается идти прямо, то в действительности он будет идти по дуге.

Указанный выше механизм («диктаторский») у осла и есть способ разрешения парадокса путём выхода за пределы навязываемых им условий.

Почти тоже самое решение предлагал Паркинсон, весьма подробно рассмотревший проблему выбора. В ситуации, когда, по мнению экспертов, ни один из претендентов не обладает перевесом, следует ввести ещё один критерий выбора. Например, спросить у секретарши, какой претендент ей больше нравится. В сущности, так поступает любой человек: столкнувшись с выбором между равноценными альтернативами, он принимается за поиски их признаков, которые можно было бы привлечь в качестве дополнительных критериев оценки и выбора. Но любые дополнительные критерии, используемые после голосования, есть, по Эрроу, проявление диктатуры.

Ситуация хорошо описана в теории катастроф: в критической ситуации (в точке бифуркации) равновесие может нарушить любой незначительный фактор, который в других ситуациях не учитывается. Но Эрроу полагает, что список критериев (факторов) конечен и не может быть произвольно дополнен «после того». Диктатором, естественно. Незначительность дополнительного фактора делает его эквивалентом монетки, используемой для выбора между двумя равноценными альтернативами.

Как всякая теоретическая модель, процедура голосования по Эрроу имеет ограниченное число переменных факторов, при которых она всегда имеет шанс придти к состоянию равновесия. В реальности же число факторов неограниченно и любой эн плюс первый фактор обязательно выведет систему из эн факторов из равновесия. Эрроу посчитал, этот дополнительный фактор обязательно будет диктаторским, во-первых, и что это плохо, во-вторых.

Вряд ли Эрроу не знал, что для разрешения парадокса необходимо выйти за рамки его условий. Вот он 6-й аксиомой и запретил этот выход (из вредности, что ли). Но есть ещё вход: для разрешения парадокса можно прибегнуть к устранению условия его возникновения. В данном случае таковым условием пересмотр пяти его аксиом. Иначе говоря, вполне возможным представляется пересмотр понимания термина «демократия». Вряд ли кто будет спорить с тем, что содержание этого понятия (как и любого иного) со временем меняется.

Всякий специалист ТРИЗ знает, что лучше устранить причину возникновения проблемы, чем бороться с её последствиями, как это предложил Эрроу (другим, естественно). Проще говоря, надо ещё до выборов исключить возникновение патовой ситуации.

Такие подходы практикуются не только среди ослов, но и, например, в виде непропорционального представительства в парламенте, когда партия, получившая относительное большинство голосов, получает абсолютное большинство мест. Ещё вариант, совсем не демократический: отстрел, подкуп, шантаж, давление. Но и это не радикальное, тем более – не демократическое, решение: даже в этих условиях возможна патовая ситуация.

Главное в стаде ослов ведь не система подсчёта голосов как таковая. В конце концов, можно придумать кучу приёмов, позволяющих если не избежать, то, хотя бы, выйти из тупикового положения. Например, заимствовав что-то из спорта. В шахматах ничья означает проигрыш претендента и сохранение короны у прежнего чемпиона. Или взять на вооружение яхтенный аналог – гонки с гандикапом. Но это спорт.

В стаде же главное – вовсе не правильный подсчёт очков. В политике, как и в бизнесе, всё решают три фактора: энергия лидера, идея и организация.

Можно ли вообще только с помощью сколь угодно изощрённой процедуры подсчёта достаточно достоверно установить наличие этих факторов? И, главное, оценить качество этих факторов?

Если продолжать вполне корректную аналогию с бизнесом, то какой продукт толкают потребителю? И кто потребитель?

Выборы – это тоже бизнес, на котором в роли покупателей выступают финансово-промышленные группы, обладающие определёнными интересами и, главное, деньгами («что хорошо для Дженерал Моторс, то хорошо для Америки»). В роли продавцов – политики и их фирмы (политические партии). Они отвечают за изготовление и поставку товара – организацию (структурирование) электората и преобразование его в голоса. Количество нужных голосов – к.п.д. обработки. Ну, а технология обработки предопределяется характеристиками ослов (сырья). В этом смысле правила подсчёта голосов – это лишь правила прозрачности, корректности подсчёта эффективности политического бизнеса.

Отсюда проблемы демократии, с тревогой отмечаемые большинством европейских социологов: каждый избиратель вынужден думать сам о себе и не иначе. А если каждый думает только о себе, то ничего большого построить не удастся. Люди становятся мелочными. Как недавно заявил некий бизнес-консультант по вопросам телевидения, такие как он, не будут воевать ни за Европу, ни за родную Голландию.

Вспомним 11-е сентября 2002 г. и его последствия в виде существенного ограничения прав и свобод американцев «ради безопасности». Вспомним также высочайший уровень преступности в США.

Так вот, лёгкость и скорость, с какой американцы пошли на ограничения своих прав, наводят на мысль, что все эти «демократические ценности» не являются такими уж органично свойственными людям. Свобода и независимость, столь органично присущие двести лет назад американским переселенцам (и основанные, кстати, на наплевательском отношении к таким же правам негров и индейцев), оказались малопригодными для жизни больших, плотных сообществ.

Демократический централизм, изобретённый при социализме, – это, конечно, плохо. Если правящая команда сама определяла, кто пополнит её ряды, и кого из себя выдвинуть, то участие прочего населения было декоративным. Но сейчас парламентарии сами устанавливают правила, по которым новички могут пополнить их ряды и за избирателями остаётся лишь право проголосовать за них. А равное право быть избранным как было, так и осталось фикцией. При достаточной консолидации парламентариев и близких к ним возникает вполне демократически избираемая диктатура. Как Гитлер, например.

Красная революция в Германии и коричневая во Франции после 1-й Мировой войны были подавлены сугубо диктаторскими методами.

Зато коричневая революция в Германии была реализована по всем канонам демократических выборов. В сегодняшней Турции голосуют вполне демократически, но если в итоге будут избраны лидеры фундаменталистской ориентации, последует военный переворот, и их сбросят. Демократически выбранный Альенде в Чили вполне диктаторски был убит Пиночетом при поддержке демократичных США.

Конечно, эти соображения не снимают проблемы Эрроу: как быть, если возникла неопределённость? Как быть, если одна половина ослов хочет идти направо, а другая – налево? Но вопрос переносится в иную область: неопределённость эта есть следствие неопределённости с долгосрочными интересами различных финансово-промышленных групп.

И, следовательно, проблема в определении этих интересов, зависящих от достоверности прогнозов эволюции страны в целом и, соответственно, разработки средств коррекции неблагоприятных тенденций. Страна одна и поэтому разброс рецептов, равно как и взаимоисключающие рецепты, говорит лишь о некорректности анализа ситуации. Ситуация, знакомая специалистам ТРИЗ по задачам в технической области: неопределённость свидетельствует о низком качестве существующих инструментов решения социальных задач в масштабе государства.

Здесь имеет место не только равенство альтернатив по всем критериям, а и равенство суммарной оценки этих критериев (что, впрочем, не исключает и полного равенства). То есть, голосующим ослам предлагается не идентичные стога как таковые, а выбор направления эволюции стада ослов. Направления эти уже в принципе не могут быть одинаковыми с точки зрения приспособления к грядущим изменениям внешней среды.

Скажем, к правому стогу вроде бы движется другое стадо ослов, у левого – наблюдаются некоторые признаки присутствия местного авторитета из семейства кошачьих, а возле среднего поблескивает что-то подозрительно похожее на оптический прицел.

Достоинства стогов очевидны, а недостатки – вероятностны и известны рядовым ослам лишь со слов лидеров партий, располагающих всегда неполными разведданными и результатами их анализа. Соответственно, результат голосования и дальнейшая судьба ослов также становятся вероятностными. Иначе говоря, практического смысла демократизм голосования не имеет. Любой вариант хорош, но и чреват. И только если не повезёт, с лидера спросят. Если будет кому и с кого.

Здесь становится очевидной функция выборов как формы обратной связи в гомеостазе социума в условиях неопределённости. Выглядит это как сопоставление прошлого состояния стада с настоящим. И лишь немного – плана и факта. А может ли вообще эта функция быть достаточно эффективной? Если учесть, что ослов объединяет в одно целое лишь общий и поэтому, как правило, простейший фактор, то не может. Особенно в вечевой форме. Парламент не так уж и отличается от вече.

Разве что профессионализмом и процедурой. Временной горизонт его видения вперёд – один срок. И опять упираемся в отсутствие инструментов ухода от «метода» проб и ошибок в больших социальных группах, которые, впрочем, плохо наработаны и на уровне малых групп – предприятий (компаний, фирм, корпораций, организаций).

Хороший индикатор неопределённости и, соответственно, качества политических инструментов, это количество партий. Если в государстве существует полсотни партий и десяток фракций (депутатских групп), что хорошего можно сказать об определённости в отношении «вектора развития» такого государства?

Правда, и наличие всего одной партии тоже ещё не говорит о том, что она располагает необходимым инструментарием. Думать же, что отсутствие такового можно заменить математическими приёмами, наивно. Или лицемерно. Разве что Эрроу так пошутил.

Не случайно же символом демократической партии США выбран именно осёл.

Похожие публикации